Die Ursprünge der Mathematik
- Jens Bott

- 20. Jan. 2024
- 5 Min. Lesezeit
Aktualisiert: 28. Sept. 2024
Im Anfang war die Zahl
Schimpansen greifen bei Revierkämpfen keine Artgenossen an, wenn die eigene Gruppe nicht mindestens um das Anderthalbfache überlegen ist. Auch Rabenvögel sind in der Lage, Größenordnungen einschätzen zu können. Diese Fähigkeit ist ein evolutionärer Vorteil bei Angriff, Verteidigung oder Futtersuche. Einige Primaten können zudem Mengen bis fünf genau unterscheiden. Doch weiter geht die Tiermathematik nicht.
Manche Wissenschaftler meinen, in einem 1960 bei Ishango im Kongo gefundenen etwa 20.000 Jahre alten Pavianknochen Beweise einer entwickelten steinzeitlichen Mathematik gefunden zu haben. In den gruppierten Kerben sehen sie entweder komplexe mathematische Strukturen oder einen Mondkalender. Doch solche Behauptungen sind höchst spekulativ und daher äußerst umstritten. Denn wenn wir die wenigen Naturvölker, betrachten, die bis vor kurzem noch isoliert als Wildbeuter auf unserem Planeten lebten, haben diese für alles, was eine Handvoll übersteigt, keine exakten Worte. Ganz offenbar spielten solche Größenordnungen in ihrem Alltag schlichtweg keine Rolle.
Eine Mathematik, die über die anderer Menschenaffen hinausgeht, gibt es nachweislich erst seit der neolithischen Revolution, der Erfindung von Ackerbau und Viehzucht. Das hängt offenbar damit zusammen, dass das menschliche Gehirn Mengen grösser fünf in der Regel nicht mehr simultan erfassen kann; das heißt, wir müssen zählen. Zählen ist die Grundlage aller Mathematik.

Als sich mit der Sesshaftigkeit erstmals komplexere soziale Strukturen bildeten, wurde das Zählen schlicht und ergreifend eine Notwendigkeit. Menschenmassen, Viehherden, Tauschhandel, Landzuteilung, Erbschaften und Steuern erforderten ein erweitertes Zahlenverständnis, um die neuen, größeren Gemeinschaften organisieren zu können. So trivial es klingt: Die Anfänge der Mathematik waren schnöde Buchhaltungssysteme, bei denen Schreiber einfache Transaktionen auf Tontafeln festhielten.
Fingerspiele
Die Schreiber hatten dabei zwei Probleme zu lösen. Zum einen galt es beim Zählen den Überblick zu behalten. Die Technik, die dazu entwickelt wurde, war so einfach und naheliegend, dass wir sie noch heute auf Bierdeckeln benutzen: Strichlisten.
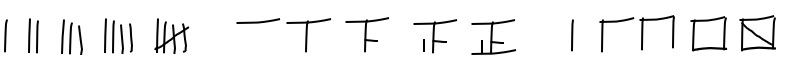

Dass Strichlisten bis heute in verschiedensten Kulturen zu Fünfergruppen zusammengefasst werden, ist kein Zufall: Es ist die Zahl der Finger einer Hand. Und auch, dass die Striche selbst wie Finger aussehen, kommt nicht von ungefähr. Kleine Kinder zeigen uns, dass es die natürlichste Sache der Welt ist, Finger als Zählhilfe zu nutzen. Fünf Finger mal zwei Hände sind der Ursprung des Dezimalsystems, das sich heute fast überall auf der Welt durchgesetzt hat. Hätten wir nur acht Finger, wäre unsere Referenz wohl ein Oktalsystem, mit dessen Logik wir dann ebenfalls keinerlei Probleme hätten. Nimmt man zu den Händen auch noch die Füße hinzu, kann man bereits bis 20 zählen. Das Zwanzigersystem war einst weit verbreitet. Davon zeugen heute noch Relikte mehrerer europäischer Sprachen, etwa das französische „quatre-vingts“ („vier Zwanziger“) für achtzig oder die dänischen Zahlwörter „tres“ und „firs“ für sechzig und achtzig als Verkürzungen von dreimal beziehungsweise viermal zwanzig.
Da bei größeren Zahlen Strichlisten und menschlicher Körper als Hilfsmittel schnell an natürliche Grenzen stoßen, kam man auf die Idee, neben den Strichen weitere Zahlensymbole zu erfinden. Mengen wie 10, 20, 30, 50, 60, 100 oder 1000 wurden bestimmte Zeichen zugewiesen. Das römische und das arabische Zahlensystem benutzen beispielsweise für die Zahl fünfzig die Symbole „L“ beziehungsweise „50“. Die Verbindung von Menge und Symbol war von nun an lediglich eine Frage der Konvention.
Die andere Herausforderung war es, die Zahl mit dem zu zählenden Objekt zu verknüpfen; es lag nahe, dies über eine einfache Zeichnung zu tun, etwa

für ein Rind oder

für einen Scheffel Weizen. Es ist kein Zufall, dass „zählen“ und „erzählen“ im Deutschen und anderen Sprachen sehr ähnlich klingen. Mathematik und Schrift haben einen gemeinsamen Ursprung; beide sind eng miteinander verwobene Kulturtechniken, die Ackerbauern und Viehzüchter zwangsläufig entwickeln mussten, um Ordnung in ihre neue, komplexere Welt zu bringen. Die ersten Schriftkundigen waren somit gleichzeitig Buchhalter, Schreiber und Rechenmeister. Die japanische Sprache erinnert uns übrigens heute noch daran, wie eng Zahl und Gezähltes miteinander verbunden sind: Je nachdem, ob Bäume, Geldscheine, Schwerter, Jahre oder Fragen gezählt werden, fordert das Japanische die Verwendung völlig unterschiedlicher Zählwörter. Reste dieser Logik haben sich auch im Deutschen erhalten, etwa wenn wir von drei Laib Brot, vier Blatt Papier oder fünf Stück Vieh sprechen.
Eine einzigartige Kulturleistung
Zwei Weizenscheffel und zwei Weizenscheffel ergeben vier Weizenscheffel. Vier Ochsen und drei Ochsen ergeben sieben Ochsen. Erst mit der Zeit offenbarte sich den Menschen, was uns heute selbstverständlich erscheint: dass zwei und zwei immer vier ergibt und vier und drei immer sieben, ganz gleich, was gezählt wird. Wie Jürgen Kaube es ausdrückte, sind „Zahlen stets Zahlen von Etwas, zugleich aber immer auch Zahlen von allem“. Einmal gedanklich von den mit ihnen verbundenen Dingen befreit, ließen sich die merkwürdigen Gebilde nun als solche betrachten und auf ihre Eigenschaften hin untersuchen. Man entdeckte Addition, Multiplikation, Subtraktion und Division als Techniken, um Zählvorgänge abzukürzen. Es zeigte sich, dass manche Zahlen ohne Rest teilbar waren, andere hingegen nicht. Es zeigte sich auch, dass verschiedene Operationen zu demselben Ergebnis führten. So lässt sich die Zahl zwölf sowohl durch drei mal vier als auch durch zwei mal sechs erzeugen. Außerdem eigneten sich die Zahlen dazu, verschiedene Dinge zueinander in Beziehung zu setzen: Wert oder Gewicht eines Ochsen ließen sich auch in Weizenscheffeln ausdrücken. Reine und angewandte Mathematik förderten eine neue Form abstrakten Denkens, die bis heute eine der herausragendsten Kulturleistungen der Menschheit bleibt.
Die Sprache der Natur
Bald zeigte sich, dass sich mit Zahlen auch die Regelhaftigkeit der Natur beschreiben ließ. Für die frühen bäuerlichen Hochkulturen war das Wissen um jahreszeitliche Rhythmen, die periodische Wiederkehr von Tagundnachtgleichen, Sommer- und Wintersonnenwende, oftmals eine Frage des Überlebens. Der Schlüssel zum Verständnis der Natur stand ganz offenbar in den Sternen. Mit Mathematik ließ sich die himmlische Ordnung erstmals aufdecken und darstellen. Die Priester-Astronomen, die anhand von Sonnenständen und Mondphasen das nächste Hochwasser an Euphrat oder Nil vorhersagen konnten, gelangten so zu Macht und Einfluss. Spätestens jetzt war Mathematik auch ein Herrschaftsinstrument geworden.
Das unschlagbare Sexagesimalsystem
Vor 4.000 Jahren war das Sexagesimalsystem, ein Stellenwertsystem, das nicht wie unser Dezimalsystem auf der Zahl zehn, sondern auf der Zahl sechzig basiert, Grundlage der babylonischen Mathematik. Das Jahr hatte nach Überzeugung der Astronomen zwischen Euphrat und Tigris 360 Tage, unterteilt in 12 Monate zu je 30 Tagen (Eine Ungenauigkeit, die natürlich schon bald Schaltmonate nötig machte.) Unsere Zeitrechnung mit 60 Sekunden und Minuten, 24 Stunden und 12 Monaten, ist ein Überbleibsel dieses Denkens, ebenso die geometrische Einteilung des Kreises in 360 Grad.

Neben seiner astronomischen Bedeutung hatte das Sexagesimalsystem aber auch noch einen ganz irdischen Vorzug, den es auf den Märkten des Zweistromlands täglich unter Beweis stellen konnte: Die Basiszahl 60 ist durch 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 und 60 ohne Rest teilbar; Güter, die nach diesem System gehandelt wurden, waren daher in den meisten Fällen leicht aufzuteilen. Das war außerordentlich hilfreich, denn mit Bruchzahlen, also Zahlen, die man beim Teilen „zerbrechen“ musste, wussten die Babylonier noch nicht so recht umzugehen.
Weiterführende Literatur:
Pyritz, Lennart (2011): „Mathematik bei Mensch und Huhn“ in: Süddeutsche Zeitung Online vom 27.07.2011.
Kaube, Jürgen (2017): „Die Anfänge von Allem“ (13. Kapitel), Rowohlt.
Pickover, Clifford A (2014): „Das Mathebuch”, Libero.



Kommentare